Question

A box contains three cards, labeled 1, 2, and 3. Two cards are chosen at random, with the first card being replaced before the second card is drawn. Let X represent the number on the first card, and let Y represent the number on the second card.

A. Find the joint probability mass function of X and Y.
B. Find the marginal probability mass functions pX(x) and pY(y).
C. Find µX and µY.
D. Find µXY.
E. Find Cov(X,Y).

Answer 1

Explanation:

Given that a box ontains three cards, labeled 1, 2, and 3.

Two cards are chosen at random, with the first card being replaced before the second card is drawn.

Let X represent the number on the first card, and let Y represent the number on the second card.

Since drawing is done with replacement, we find that X and Y are independnet

A) Joint pdf of x and y are

y x 0 1 2 3 Total

0 0.0625 0.0625 0.0625 0.0625 0.25

1 0.0625 0.0625 0.0625 0.0625 0.25

2 0.0625 0.0625 0.0625 0.0625 0.25

3 0.0625 0.0625 0.0625 0.0625 0.25

Total 0.25 0.25 0.25 0.25

B) Pdf of X is

x 0 1 2 3

p 0.25 0.25 0.25 0.25

and Y also will have same pdf

C)
`\mu_x = 0.25(0+1+2+3) = 1.5\\\mu_y = 0.25(0+1+2+3) = 1.5`

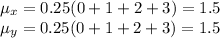
D)
`\mu_(xy ) =E(x) E(y) = 2.25`

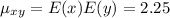
E) Cov (x,y) =0 since X and Y are independent