Question

Park officials make predictions of times to the next eruption of a particular​ geyser, and collect data for the errors​ (minutes) in those predictions. The display from technology available below results from using the prediction errors to test the claim that the mean prediction error is equal to zero. Comment on the accuracy of the predictions. Use a 0.05 significance level. Identify the null and alternative​ hypotheses, test​ statistic, P-value, and state the final conclusion that addresses the original claim.

Answer 1

a) Null hypothesis:
`\mu =0`

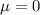
Alternative hypothesis:
`\mu \\eq 0`

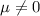
b) t =-7.44

c)
`p_v = 2*P(t_(98)<-7.44)<0.0001`

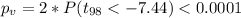
d) Reject Null hypothesis. The is enough evidence to conclude that the mean prediction error is not equal to 0.

We reject the null hypothesis because the
`p_v <\alpha`. So we can conclude that the difference is significantly different from 0 at 5% of significance.

Explanation:

Assuming this output:

`t_(difference)=-0.395`

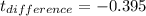
t(observed value) =-7.44

t(Critical value )= 1.984

DF = 98

p value (two tailed) < 0.0001

`\alpha =0.05`

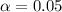
a) What are the null and alternative hypothesis

Null hypothesis:
`\mu =0`

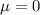
Alternative hypothesis:
`\mu \\eq 0`

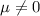
The reason is because the output says a bilateral test so for this case w eselect this option.

b) Identify the statistic

The correct formula for the statistic is given by:

`t=\frac{\bar X_1 -\bar X_2 -0}{\sqrt{((s^2_1)/(n_1)+(s^2_2)/(n_2))}}`

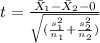
Based on the output the calculated value its t =-7.44

c) Identify the p value

We have the degrees of freedom given 98

Based on the alternative hypothesis the p value is given by:

`p_v = 2*P(t_(98)<-7.44)<0.0001`

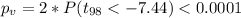
d) State the final conclusion that addresses the original claim

Reject Null hypothesis. The is enough evidence to conclude that the mean prediction error is not equal to 0.

We reject the null hypothesis because the
`p_v <\alpha`. So we can conclude that the difference is significantly different from 0 at 5% of significance.