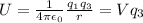The electric potential is a scalar unit, so we don't have to struggle with the vectors. The formula that gives electric potential is
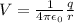
1) At point a, the electric potential is the sum of the potentials due to q1 and q2. So,

The distance from the center of the square to one of the corners is

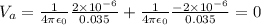
The answer is zero, because the point charges are at equal distances and their magnitudes are also equal but their directions are opposite.
2)
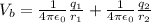
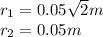
![V_b = (1)/(4\pi\epsilon_0)(2*10^(-6))/(0.05\sqrt2) + (1)/(4\pi\epsilon_0)(-2*10^(-6))/(0.05)\\V_b = (1)/(4\pi\epsilon_0)(2*10^(-6))/(0.05) ((1)/(\sqrt2)-1)\\V_b = (1)/(4\pi\epsilon_0) (4* 10^(-5))(-0.29)\\V_b = (-(2.9*10^(-6))/(\pi\epsilon_0))[tex]</p><p></p><p>3) The work done on q3 by q1 and q2 is equal to the difference between energies. This is the work-energy theorem. So,</p><p>[tex]W = U_b - U_a]()