Answer:
![E[R]](https://img.qammunity.org/2020/formulas/mathematics/college/ofcowkxrra1xwb50zx398t22jxlpb6gtli.png) = 99 Ω
= 99 Ω
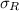 = 2.3094 Ω
= 2.3094 Ω
P(98<R<102) = 0.5696
Explanation:
The mean resistance is the average of edge values of interval.
Hence,
The mean resistance,
![E[R] = (a+b)/(2) = (95+103)/(2) = (198)/(2)](https://img.qammunity.org/2020/formulas/mathematics/college/1lyo345mf4tbw5m0towa5u4djibp7xo2gr.png) = 99 Ω
= 99 Ω
To find the standard deviation of resistance, we need to find variance first.
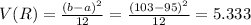
Hence,
The standard deviation of resistance,
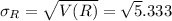 = 2.3094 Ω
= 2.3094 Ω
To calculate the probability that resistance is between 98 Ω and 102 Ω, we need to find Normal Distributions.
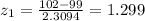
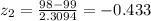
From the Z-table, P(98<R<102) = 0.9032 - 0.3336 = 0.5696