Question

Resistors are labeled 100 Ω. In fact, the actual resistances are uniformly distributed on the interval (95, 103). Find the mean resistance. Find the standard deviation of the resistances. Find the probability that the resistance is between 98 and 102 Ω. Suppose that resistances of different resistors are independent. What is the probability that three out of six resistors have resistances greater than 100 Ω?

Answer 1

`E[R]` = 99 Ω

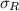`\sigma_R` = 2.3094 Ω

P(98<R<102) = 0.5696

Explanation:

The mean resistance is the average of edge values of interval.

Hence,

The mean resistance,
`E[R] = (a+b)/(2)  = (95+103)/(2) = (198)/(2)` = 99 Ω

To find the standard deviation of resistance, we need to find variance first.

`V(R) = ((b-a)^2)/(12) =((103-95)^2)/(12) = 5.333`

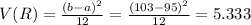
Hence,

The standard deviation of resistance,
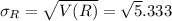`\sigma_R = √(V(R)) = \sqrt5.333` = 2.3094 Ω

To calculate the probability that resistance is between 98 Ω and 102 Ω, we need to find Normal Distributions.

`z_1 = (102-99)/(2.3094) = 1.299`

`z_2 = (98-99)/(2.3094) = -0.433`

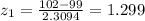
From the Z-table, P(98<R<102) = 0.9032 - 0.3336 = 0.5696