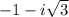Question

Find all the zeros of the equation. -x^3-3x^2=6x+4

Answer 1

Explanation:

the answer is A, just took the test

Answer 2

The zeros of given expression
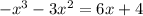`-x^3-3x^2=6x+4` is -1,
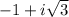`-1+i√(3)` and
`-1-i√(3)`

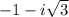
Explanation:

Given expresssion is
`-x^3-3x^2=6x+4`

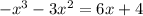
To find zeros of given expression we have to equate the expression to zero.

ie.,
`-x^3-3^2-6x-4=0`

`-(x^3+3x^2+6x+4)=0`

`x^3+3x^2+6x+4=0`

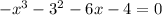
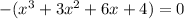
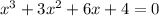
By using synthetic division

-1 | 1 3 6 4

| 0 -1 -2 -4

|________________

1 2 4 0

Therefore (x+1) is a zero

Now the quadratic equation is
`x^2+2x+4=0`

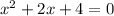
For quadratic equation
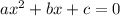`ax^2+bx+c=0` we have

`x=(-b\pm √(b^2-4ac))/(2a)`

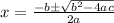
Here a=1 ,b=2 and c=4 now substitute the values

`x=(-2\pm √(2^2-4(1)(4)))/(2(1))`

`x=(-2\pm √(4-16))/(2)`

`x=(-2\pm √(-12))/(2)`

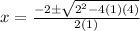
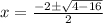
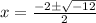
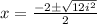`x=(-2\pm √(12i^2))/(2)` where
`i^2=-1`

`x=(-2\pm i √(4* 3))/(2)`

`x=(-2\pm i √(4)√(3))/(2)`

`x=(-2\pm 2i√(3))/(2)`

`x=2*((-1\pm i√(3)))/(2)`

`x=-1\pm i√(3)`

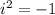
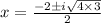
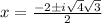
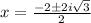
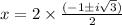
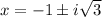
Therefore
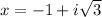`x=-1+i√(3)` and
`x=-1-i√(3)`

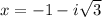
Therefore the zeros are -1,
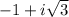`-1+i√(3)` and
`-1-i√(3)`