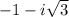Answer:
The zeros of given expression
 is -1,
is -1,
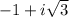 and
and
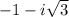
Explanation:
Given expresssion is

To find zeros of given expression we have to equate the expression to zero.
ie.,
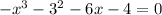

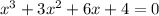
By using synthetic division
-1 | 1 3 6 4
| 0 -1 -2 -4
|________________
1 2 4 0
Therefore (x+1) is a zero
Now the quadratic equation is

For quadratic equation
 we have
we have

Here a=1 ,b=2 and c=4 now substitute the values
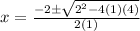

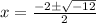
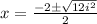 where
where

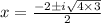
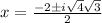

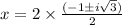
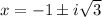
Therefore
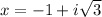 and
and
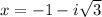
Therefore the zeros are -1,
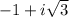 and
and