Question

For the class of 2013's prom Norman's dress shop sold cheaper dresses for $90 each and more expensive dresses for $140 each. They took in $5250 and sold 20 more of the cheaper dresses than the expensive dresses. How many of each kind did they sell? Simply need help setting up the equations. I can solve them on my own.

Answer 1

Number of cheaper dresses sold is 35

Number of expensive dresses sold is 15

Explanation:

Given:

Cost of cheaper dresses = $90

Cost of expensive dresses = $140

Total cost of the dresses = $5250

To Find:

Number of cheaper dress = ?

Number of expensive dress = ?

Solution:

Let

The number of cheaper dresses be x

The number of expensive dresses be y

(Number of cheaper dresses X cost of cheap dress) + (Number of Expensive dresses X cost of expensive dress) = $5250

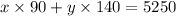`x *90 +y * 140 = 5250`= $5250

It is given that the 20 more of the cheaper dresses than the expensive dresses is sold

So,

number of cheaper dress = 20 + number of expensive dress

x = 20 + y---------------------------------------(1)

`(20+y) *90 +y * 140 = 5250 = 5250`

`(20 * 90 +y* 90) +y * 140= 5250`

`1800 + 90y+ 140y = 5250`

`1800 + 230y = 5250`

`230y =5250 -1800`

`230y = 3450`

`y = (3450)/(230)`

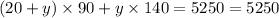
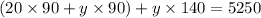
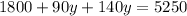
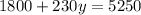
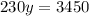
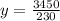
y = 15

Substituting y in (1)

x = 20 +15

x= 35