Question

An engineer has an odd-shaped 13.5 kg object and needs to find its rotational inertia about an axis through its center of mass. The object is supported on a wire stretched along the desired axis. The wire has a torsion constant κ = 0.618 N·m. If this torsion pendulum oscillates through 28 cycles in 58.1 s, what is the rotational inertia of the object?

Answer 1

I = 0.0674 kg.m²

Step-by-step explanation:

given,

mass = 13.5 Kg

torsion constant = k = 0.618 N.m

number of cycle = 28

time = 58.1 s

Time of one cycle

`T = (58.1)/(28)`

`T =2.075\ s`

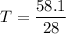
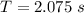
we know,

`T = 2\pi\sqrt{(I)/(k)}`

`I = k ((T)/(2\pi))^2`

`I =0.618* (T^2)/(4\pi^2)`

`I =0.618* (2.075^2)/(4\pi^2)`

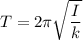
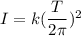
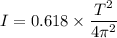
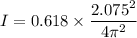
I = 0.0674 kg.m²

the rotational inertia of the object is equal to I = 0.0674 kg.m²