Answer:
I = 0.0674 kg.m²
Step-by-step explanation:
given,
mass = 13.5 Kg
torsion constant = k = 0.618 N.m
number of cycle = 28
time = 58.1 s
Time of one cycle
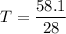
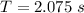
we know,
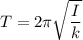
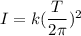
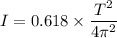

I = 0.0674 kg.m²
the rotational inertia of the object is equal to I = 0.0674 kg.m²