Question

What is the value of cos(x) if tan ( x)= -2 and x is in quadrant of IV?

Answer 1

`cos(x)=(√(5))/(5)`

Explanation:

we have that

`tan(x)=-2`

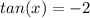
The angle x is in quadrant IV

That means ---> The value of cos(x) is positive and the value of sin(x) is negative

Remember that

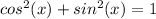`cos^2(x)+sin^2(x)=1` ----> equation A

`tan(x)=(sin(x))/(cos(x))`

so

`-2=(sin(x))/(cos(x))`

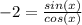
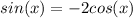`sin(x)=-2cos(x)` ----> equation B

substitute equation B in equation A

`cos^2(x)+(-2cos(x))^2=1`

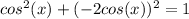
solve for cos(x)

`cos^2(x)+4cos^2(x)=1`

`5cos^2(x)=1`

`cos^2(x)=(1)/(5)`

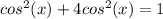
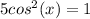
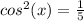
square root both sides

`cos(x)=\pm(1)/(√(5))`

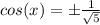
but remember that the value of cos(x) is positive (IV quadrant)

`cos(x)=(1)/(√(5))`

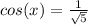
simplify

`cos(x)=(√(5))/(5)`