Question

The lumen output was determined for each of I = 3 different brands of lightbulbs having the same wattage, with J = 8 bulbs of each brand tested. The sums of squares were computed as SSE = 4776.3 and SSTr = 599.5. State the hypotheses of interest (including word definitions of parameters).

Answer 1

Explanation:

Hello!

The study variable is

X: Lumen of a bulb of the i brand. i=3

There are 3 populations of bulbs, Brand 1, Brand 2 and brand 3.

The objective is to test if the population means are equal.

The study parameters are:

μ₁: population mean lumen of the population of light bulbs of brand 1.

μ₂: population mean lumen of the population of light bulbs of brand 2.

μ₃: population mean lumen of the population of light bulbs of brand 3.

The hypothesis is:

H₀:μ₁= μ₂= μ₃= μ

H₁: At least one of the population means is different.

To test this hypothesis, considering the given information, I'll use an ANOVA test, then the statistic is defined as:

`F= (MSTr)/(MSerror)`~
`F_((I-1)(J-1))`

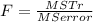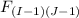
Rejection region

This region is always one-tailed (right), the statistic is constructed as the mean square of the treatments divided by the mean square of the error, if the number of F is big, this means that the treatments have more effect over the populations. If the value of F is small, this means that there is no difference between the variability caused by the treatments and the one caused by the residues.

Since there is no significance level specified, I'll use α: 0.05

`F_((I-1);(J-1); 1 - \alpha ) = F_(2; 7; 0.95) = 19.35`

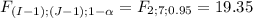
You will reject the null hypothesis when F
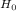`_(H_0)` ≥ 19.35

To calculate the statistic value you need to calculate the Mean Square of Treatments and the Mean Square of errors:

MSTr= SSTr/DfTr = 599.5/2= 299.75

MSerror= SSerror/Dferror= 4776.3/5= 955.26

F
`_(H_0)`=
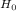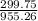`(299.75)/(955.26)`= 0.31

At this level the decision is to not reject the null hypothesis.

I hope it helps!