Answer:
The center of the circle is c=50 and radius of the circle is

Explanation:
Given circle equation is

Equation (1) can be written as

we know that the equation of the circle is of the form

with centre (-g,-f) and radius=
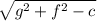
when, g,f and c are constants
Now comparing the (2) and (3) equations we get 2g=-4
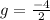
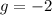
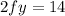
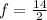
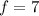
and
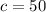
Now to find the centre and radius of the given circle equation, substituting the values of g,f,c in the formulae of centre and radius
centre=(-g,-f)
=(-(-2),-7)
centre=(2,7)
Radius=
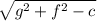
=
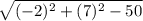
=
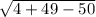
=
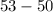
Radius=
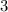
The center of the circle is c=50 and the radius of the circle equation
