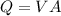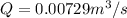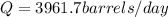Question

The present pumping rate of crude oil through the Alaska Pipeline, with an ID of 48 in, is 550,000 barrels per day (1 barrel is 42 U. S. gallons).

(a) Is this a turbulent flow?


(b) What would be the maximum rate if the flow were constrained to be laminar?

Answer 1

To solve this problem it is necessary to apply the concepts related to the Reynolds number and the Flow.

The Reynolds number can be defined as

`Re = (V\rho D)/(\mu)`

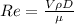
Where,

V = Velocity of Fluid

D = Diameter

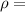`\rho =` Density

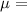`\mu =`Viscosity.

At the same time we have that the Flow charge is given as

`Q = VA \rightarrow V = (Q)/(A)`

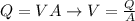
Where,

V = Velocity

A = Cross-sectional Area

Our values are given as:

`\rho = 998kg/m^3`

`\mu = 0.0038kg/m\cdot s`

`d = 1/8`

`Q = 550000 barrels/day  = 1.012m^3/s`

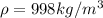
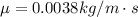
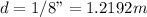
PART A) Using these two relationships we can find if the flow is turbulent. Recall that according to Reynolds, if its value is greater than 4000 the flow is turbulent. From 2000 to 4000 transitory and less than 2000 laminar.

`V = (Q)/(A)`

`V = (1.012)/((\pi)/(4)*1.2191^2)`

`V = 0.867m/s`

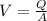
Now replacing at Reynolds equation:

`Re = (V\rho D)/(\mu)`

`Re = (0.867*1.2192*998)/(0.0038)`

`Re = 277613`

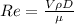
The flow is turbulent.

PART B) For the flow to be laminar we must modify the flow rate therefore

`Re = 2000`

`2000 = (V*1.2192*998)/(0.0038)`

`V = 6.245*10^(-3)m/s`

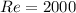
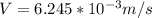
Substituting to find the Flow charge

`Q = VA`

`Q = (\pi)/(4)*1.2192^2*0.006245`

`Q = 0.00729m^3/s`

`Q = 3961.7 barrels/day`