Question

Find three consecutive integers such that the square of the first, increased by the last, is 32.

Answer 1

`\huge\boxed{5, 6, 7}`

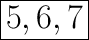
Explanation:

In order to find the 3 consecutive digits here, we need to note that consecutive numbers are numbers that appear as the number right above each other.

For example: 2, 3, 4 are consecutive, as are -10, -9, -8.

We can assign the first term a variable, let's do x. Since we know the next two terms are consecutive, we can define them with
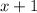`x+1` and
`x+2`.

`x, (x+1), (x+2)`

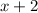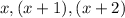
We also know that the first number squared, increased by the last, is 32. This can be modeled by the equation

`x^2 + (x+2) = 32`

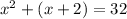
Let's solve for x in that equation by using the XBOX Method in quadratics.

• 
  `x^2 + x + 2 = 32`
• 
  `x^2 + x - 30 = 0`
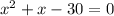
• The product of the two roots will be c (-30) and their sum will be b (1).
• 
  `-5 \cdot 6 = -30`
• 
  `-5 + 6 = 1`
• 
  `(x-5)(x+6)`
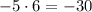
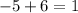
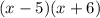
• Zeroes of the function:
  `5, -6`

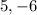
Now that we know two values of x that might work, we need to plug them into our equation to test if they actually do work.

5

`5^2 + (5+2) = 32\\\\ 25 + 7 = 32 \ \checkmark`

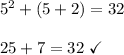
-6

`-6^2 + (-6+2) = 32 \\\\ -36 + -4 = 32 \ *`

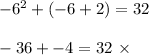
We can see here that -6 won't work as it doesn't satisfy our equation. However, 5 does work. That means our first number is 5, making our next two numbers 6 and 7.

Hence - 5, 6, 7.

Hope this helped!