Question

Lloyd's Cereal company packages cereal in 1 pound boxes (16 ounces). A sample of 16 boxes is selected at random from the production line every hour, and if the average weight is less than 15 ounces, the machine is adjusted to increase the amount of cereal dispensed. If the mean for 1 hour is 1 pound and the standard deviation is 0.1 pound, what is the probability that the amount dispensed per box will have to be increased?

Answer 1

The probability that the amount dispensed per box will have to be increased is 0.0062.

Explanation:

Consider the provided information.

Sample of 16 boxes is selected at random.

If the mean for 1 hour is 1 pound and the standard deviation is 0.1

1 Pound = 16 ounces , then 0.1 Pound = 16/10 = 1.6 ounces

Thus: μ = 16 ounces and σ = 1.6 ounces.

Compute the test statistic
`z=(\bar x-\mu)/((\sigma)/(√(n)))`

`z=(15-16)/((1.6)/(√(16)))`

`z=(-1)/((1.6)/(4))`

`z=(-1)/(0.4)`

`z=-2.5`

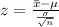
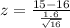
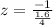
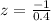
By using the table.

P value = P(Z<-250) = 0.0062

Thus, the probability that the amount dispensed per box will have to be increased is 0.0062.