Question

The Sun orbits the center of the Galaxy in 225 million years at a distance of 26,000 lightyears. Given that a^3 = (M1 +M2) x P^2, where a is the semimajor axis in AU and P is the orbital period in years, what is the mass of the Galaxy within the Sun’s orbit?

Answer 1

According to Kepler third law the relation between orbital period and radio of matter in the Galaxy is given by

`a^3 = (M_1+M_2)p^2`

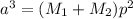
Where,

a = Radius of start orbit

p = Orbital Period

M = Total mass in a sphere of radius centered on galactic center

Our values are given as

`a = 26000ly ((9.461*10^(15)m)/(1LY)) = 2.45*10^(20)m`

`p = 225million year = 225*10^6 year`

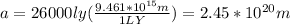
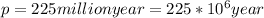
Replacing we have,

`M = (2.45*10^(20))/(225*10^6)`

`M = 1.088*10^(12)M_(sun)`

`M = 108Billion M_(sun)`

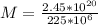
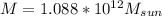
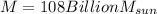
Therefore the mass of the galaxy within the sun's orbit is 108Billion the mass of the sun.