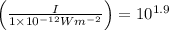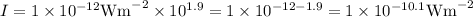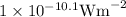Question

A sound is recorded at 19 decibels. What is the intensity of the sound?

1 x 10^-8.7 W/m^2
1 x 10^-10.1 W/m^2
1 x 10^-11.9 W/m^2
1 x 10^-9.4 W/m^2

Answer 1

`1 * 10^(-10.1) \mathrm{Wm}^(-2)` is the intensity of the sound.

Answer: Option B

Step-by-step explanation:

The range of sound intensity that people can recognize is so large (including 13 magnitude levels). The intensity of the weakest audible noise is called the hearing threshold. (intensity about
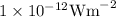`1 * 10^(-12) \mathrm{Wm}^(-2)`). Because it is difficult to imagine numbers in such a large range, it is advisable to use a scale from 0 to 100.

This is the goal of the decibel scale (dB). Because logarithm has the property of recording a large number and returning a small number, the dB scale is based on a logarithmic scale. The scale is defined so that the hearing threshold has intensity level of sound as 0.

`\text { Intensity }(d B)=(10 d B) * \log _(10)\left((I)/(I_(0))\right)`

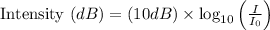
Where,

I = Intensity of the sound produced

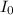`I_(0)` = Standard Intensity of sound of 60 decibels =
`1 * 10^(-12) \mathrm{Wm}^(-2)`

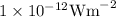
So for 19 decibels, determine I as follows,

`19 d B=(10 d B) * \log _(10)\left((I)/(1 * 10^(-12) W m^(-2))\right)`

`\log _(10)\left(\frac{1}{1 * 10^(-12) \mathrm{Wm}^(-2)}\right)=(19)/(10)`

`\log _(10)\left(\frac{1}{1 * 10^(-12) \mathrm{Wm}^(-2)}\right)=1.9`

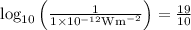
When log goes to other side, express in 10 to the power of that side value,

`\left((I)/(1 * 10^(-12) W m^(-2))\right)=10^(1.9)`

`I=1 * 10^(-12) \mathrm{Wm}^(-2) * 10^(1.9)=1 * 10^(-12-1.9)=1 * 10^(-10.1) \mathrm{Wm}^(-2)`