Question

If solid NaCl is added to a saturated water solution of PbCl2 at 20o C, a precipitate is formed. How would this affect the value of the Ksp for [Pb2+][Cl-] in solution? The Ksp increases. The Ksp decreases. The Ksp remains the same. none of the above.

Answer 1

The
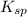`K_(sp)` remains the same

Step-by-step explanation:

Let's look at what actually happens in this scenario. Before we dive into the explanation, remember the principle of Le Chatelier: for a system at equilibrium, a specific disturbance in molarity/volume/pressure of any species in equilibrium would cause the equilibrium to shift towards the side that minimizes such a disturbance.

To begin with, we have a saturated water solution of lead(II) chloride. A saturated solution means that at the given temperature we have a maximum amount of lead(II) chloride that could dissolve in the given volume of water.

Since lead(II) chloride is not highly soluble, we have an equilibrium between the precipitate and the dissociated ions:

`PbCl_2(s)`⇄
`Pb^(2+)(aq)+2Cl^-(aq)`

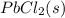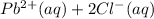
Now we're adding NaCl to this solution. Sodium chloride is a sparingly soluble salt which readily dissociates into sodium and chloride ions:

`NaCl(aq)\rightarrow Na^+ (aq)+Cl^- (aq)`

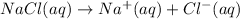
Notice that sodium chloride increases the concentration of chloride ions in the solution, so the equilibrium between the precipitate and its ions is disturbed.

According to the principle of Le Chatelier, due to an increase in chloride ions, the equilibrium would be disturbed and the system would tend to decrease it in order to restore the equilibrium. Hence, the equilibrium shifts towards the precipitate forming more of the precipitate and decreasing the amount of lead(II) cation, as well as the excess of chloride ions. This is also called the common ion effect: the common ion decreases the solubility of a salt.

However, it only decreases the solubility of the salt but not the solubility product constant defined as:

`K_(sp)=[Pb^(2+)][Cl^-]^2`

A decrease in lead(II) concentration is compensated by the excess of chloride. The solubility product is only temperature-dependent, just as any other equilibrium constant, so it doesn't depend on the molarity of chloride or lead(II) ions.

Solubility, on the other hand, is equal to:

`S=[Pb^(2+)]=(K_(sp))/([Cl^-]^2)`

And, as you can see, it decreases, as K is kept constant and we have an increase in chloride.