Question

Could someone help me tell me which ones are proportional and which ones are not? please ​

Answer 1

Table a represent a proportional relationship

Table b represent a proportional relationship

Table c not represent a proportional relationship

Table d not represent a proportional relationship

Table e represent a proportional relationship

Table f not represent a proportional relationship

Explanation:

we know that

A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
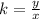`k=(y)/(x)` or
`y=kx`

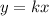
Verify each table

Find the value of the constant of proportionality k for each ordered pair

If all the values of k are equal, then the table represent a proportional relationship

`k=(y)/(x)`

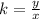
Table a

For x=2, y=14 ---->
`k=(14)/(2)=7`

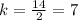
For x=5, y=35 ---->
`k=(35)/(5)=7`

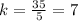
For x=7, y=49 ---->
`k=(49)/(7)=7`

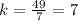
For x=10, y=70 ---->
`k=(70)/(10)=7`

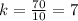
All the values of k are equal

therefore

The table a represent a proportional relationship

Table b

For x=-10, y=50 ---->
`k=(50)/(-10)=-5`

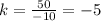
For x=-2, y=10 ---->
`k=(10)/(-2)=-5`

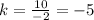
For x=4, y=-20 ---->
`k=(-20)/(4)=-5`

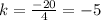
For x=14, y=-70 ---->
`k=(-70)/(14)=-5`

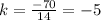
All the values of k are equal

therefore

The table b represent a proportional relationship

Table c

For x=-1, y=-24 ---->
`k=(-24)/(-1)=24`

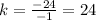
For x=2, y=48 ---->
`k=(48)/(2)=24`

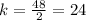
For x=4, y=90 ---->
`k=(90)/(4)=22.5`

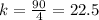
For x=8, y=192 ---->
`k=(192)/(8)=24`

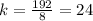
All the values of k are not equal

therefore

The table c not represent a proportional relationship

Table d

For x=-6, y=12 ---->
`k=(12)/(-6)=-2`

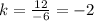
For x=-3, y=6 ---->
`k=(6)/(-3)=-2`

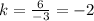
For x=3, y=-6 ---->
`k=(-6)/(3)=-2`

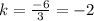
For x=6, y=-10 ---->
`k=(-10)/(6)=-1.67`

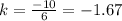
All the values of k are not equal

therefore

The table d not represent a proportional relationship

Table e

For x=2, y=13.5 ---->
`k=(13.5)/(2)=6.75`

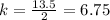
For x=5, y=33.75 ---->
`k=(33.75)/(5)=6.75`

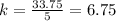
For x=10, y=67.5 ---->
`k=(67.5)/(10)=6.75`

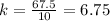
For x=15, y=101.25 ---->
`k=(101.25)/(15)=6.75`

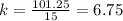
All the values of k are equal

therefore

The table e represent a proportional relationship

Table f

For x=-4, y=-38 ---->
`k=(-38)/(-4)=9.5`

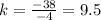
For x=-1, y=-9.5 ---->
`k=(-9.5)/(-1)=9.5`

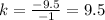
For x=2, y=19 ---->
`k=(19)/(2)=9.5`

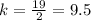
For x=3, y=27 ---->
`k=(27)/(3)=9`

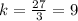
All the values of k are not equal

therefore

The table f not represent a proportional relationship