Answer:
Table a represent a proportional relationship
Table b represent a proportional relationship
Table c not represent a proportional relationship
Table d not represent a proportional relationship
Table e represent a proportional relationship
Table f not represent a proportional relationship
Explanation:
we know that
A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
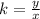 or
or

Verify each table
Find the value of the constant of proportionality k for each ordered pair
If all the values of k are equal, then the table represent a proportional relationship
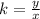
Table a
For x=2, y=14 ---->
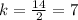
For x=5, y=35 ---->

For x=7, y=49 ---->
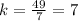
For x=10, y=70 ---->

All the values of k are equal
therefore
The table a represent a proportional relationship
Table b
For x=-10, y=50 ---->

For x=-2, y=10 ---->
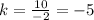
For x=4, y=-20 ---->
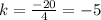
For x=14, y=-70 ---->
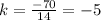
All the values of k are equal
therefore
The table b represent a proportional relationship
Table c
For x=-1, y=-24 ---->
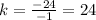
For x=2, y=48 ---->
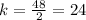
For x=4, y=90 ---->
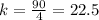
For x=8, y=192 ---->
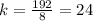
All the values of k are not equal
therefore
The table c not represent a proportional relationship
Table d
For x=-6, y=12 ---->
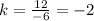
For x=-3, y=6 ---->
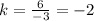
For x=3, y=-6 ---->
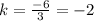
For x=6, y=-10 ---->
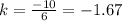
All the values of k are not equal
therefore
The table d not represent a proportional relationship
Table e
For x=2, y=13.5 ---->
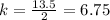
For x=5, y=33.75 ---->

For x=10, y=67.5 ---->
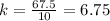
For x=15, y=101.25 ---->
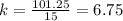
All the values of k are equal
therefore
The table e represent a proportional relationship
Table f
For x=-4, y=-38 ---->
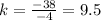
For x=-1, y=-9.5 ---->
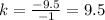
For x=2, y=19 ---->
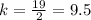
For x=3, y=27 ---->
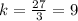
All the values of k are not equal
therefore
The table f not represent a proportional relationship