Answer:
1.
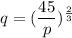
2.
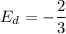
Explanation:
The given demand equation is
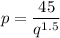
where p is the price (in dollars) per quarter-chicken serving and q is the number of quarter-chicken servings that can be sold per hour at this price.
Part 1 :
We need to Express q as a function of p.
The given equation can be rewritten as

Using the properties of exponent, we get
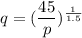
![[\because x^n=a\Rightarrow x=a^{(1)/(n)}]](https://img.qammunity.org/2020/formulas/mathematics/high-school/81bwxq6keq2exbkx6dx6nqjfbloj9f6agl.png)
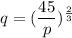
Therefore, the required equation is
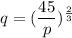 .
.
Part 2 :
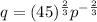
Differentiate q with respect to p.
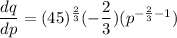
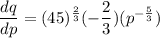
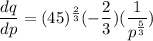
Formula for price elasticity of demand is

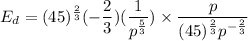
Cancel out common factors.
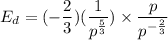
Using the properties of exponents we get
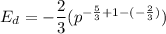

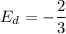
Therefore, the price elasticity of demand is -2/3.