Answer:
The probability that Smith will lose his first 5 bets is 0.15
The probability that his first win will occur on his fourth bet is 0.1012
Explanation:
Consider the provided information.
A roulette wheel consisting of 38 numbers 1 through 36, 0, and double 0. Smith always bets that the outcome will be one of the numbers 1 through 12,
It is given that Smith always bets on the numbers 1 through 12.
There are 12 numbers from 1 to 12.
Thus, the probability of success (winning) is=
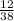
The probability of not success (loses) is=
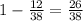
Part (A) Smith will lose his first 5 bets.
The probability that Smith loses his first 5 bets is,

Hence, the probability that Smith will lose his first 5 bets is 0.15
Part (B) His first win will occur on his fourth bet?
Smith’s first win occurring on the fourth bet means that he loses the first 3 bets and wins on the fourth bet. That is,
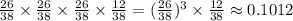
Hence, the probability that his first win will occur on his fourth bet is 0.1012