Question

A monoenergetic beam of electrons is incident on a single slit of width 0.500 nm. A diffraction pattern is formed on a screen 25.0 cm from the slit.

If the distance between successive minima of the diffraction pattern is 2.10 cm, what is the energy of the incident electrons?

Answer 1

KE=1.366×10⁻¹⁶J or

KE=854ev

Step-by-step explanation:

single slit diffraction pattern occur where sinФ=mλ/a for m=±1,±2,±3,.......

Here λ is wavelength

The spacing between successive minima is then

Δy=
`y_(m+1)-y_(m)`

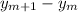
Δy=λ(L/a)

as given Δy=2.10cm, L=25cm and a=0.500nm

so for λ

λ=Δy(a/L)

`=(2.10*10^(-2)m )(((0.500*10^(-9)m))/(25*10^(-2)m) )`

λ=4.2×10⁻¹¹m

The momentum of one of these electrons is then

p=h/λ

`p=(6.63*10^(-34) )/(4.2*10^(-11))\\ p=1.578*10^(-23)kgm/s`

Assuming the electron is non-relativistic, its kinetic energy is

`KE=p^(2)/2m_(e)\\  KE=((1.578*10^(-23) )^(2) )/(2(9.11*10^(-31)))\\ KE=1.366*10^(-16)J`

Convert joules into electronvolt we get

KE=854ev