Answer:
KE=1.366×10⁻¹⁶J or
KE=854ev
Step-by-step explanation:
single slit diffraction pattern occur where sinФ=mλ/a for m=±1,±2,±3,.......
Here λ is wavelength
The spacing between successive minima is then
Δy=
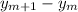
Δy=λ(L/a)
as given Δy=2.10cm, L=25cm and a=0.500nm
so for λ
λ=Δy(a/L)
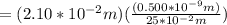
λ=4.2×10⁻¹¹m
The momentum of one of these electrons is then
p=h/λ
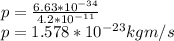
Assuming the electron is non-relativistic, its kinetic energy is
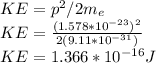
Convert joules into electronvolt we get
KE=854ev