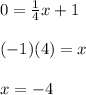Question

What is the zero of the linear function below?

Answer 1

Answer:
`x=-4`

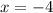
Explanation:

Remember that the line intersects the x-axis when
`y=0`.Therefore, the zero of a linear function is the value of the variable "x" when the value of "y" is zero.

The equation of the line in Slope-Intercept form is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

In this case, given the graph of the function,you can identify that the y-intercept is:

`b=1`

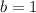
By definition, the slope can be calculated with this formula:

`m=(y_2-y_1)/(x_2-x_1)`

Then, in order to find the slope, you can pick the points (4,2) and (-8,-1) and say that:

`y_2=-1\\y_1=2\\\\x_2=-8\\x_1=4`

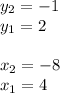
So, substituting these values into the formula, you get:

`m=(-1-2)/(-8-4)=(1)/(4)`

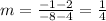
Then the linear function has this form:

`y=(1)/(4)x+1`

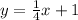
Finally, in order to find the x-intercept, you can substitute
`y=0` into the function and solve for "x". This is:

`0= (1)/(4)x +1\\\\(-1)(4)=x\\\\x=-4`