Question

A 1.0 kg piece of copper with a specific heat of cCu=390J/(kg⋅K) is placed in 1.0 kg of water with a specific heat of cw=4190J/(kg⋅K). The copper and water are initially at different temperatures. After a sufficiently long time, the copper and water come to a final equilibrium temperature. Part A Which of the following statements is correct concerning the temperature changes of both substances? (Ignore the signs of the temperature changes in your answer.) Which of the following statements is correct concerning the temperature changes of both substances? (Ignore the signs of the temperature changes in your answer.) The temperature change of the copper is equal to the temperature change of the water. The temperature change of the water is greater than the temperature change of the copper. The temperature change of the copper is greater than the temperature change of the water.

Answer 1

The temperature change of the copper is greater than the temperature change of the water.

Step-by-step explanation:

deltaQ = mc(deltaT)

Where,

delta T = change in the temperature

m =mass

c = heat capacity

`((deltaT)_(Cu))/((deltaT)_(w))=(4190J/kg.K)/(390J/kg.K)\\ \\(deltaT)_(Cu)=10.74(deltaT)_(w)`

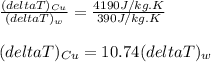
The temperature change in the copper is nearly 11 times the temperature change in the water.

So, the correct option is,

The temperature change of the copper is greater than the temperature change of the water.

Hope this helps!