Question

Six hundred chances are sold at ​$3 apiece for a raffle. There is a grand prize of ​$700​, two second prizes of ​$200​, and five third prizes of ​$50. First calculate the expected value of the lottery. Determine whether the lottery is a fair game. If the game is not​ fair, determine a price for playing the game that would make it fair.

Answer 1

Expected net gain is -$0.75. Not a fair game. Appropriate price is $2.25.

Explanation:

There is 1 in 600 chance to win the grand price (1/600)

There are 2 in 600 chance to win the 2nd price (2/600 = 1/300)

There are 5 in 600 chance to win the 3rd price (5/600 = 1/120)

We can use these probability to calculate the expected gain from this game

`E_g = 700(1)/(600) + 200*(1)/(300) + 50*(1)/(120) = \$2.25`

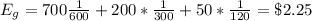
Since the cost to play is $3, the expected net gain from this game is

$2.25 - $3 = -$0.75

So this game is not fair as the player is losing money. The appropriate price should instead be $2.25