Answer:
Expected net gain is -$0.75. Not a fair game. Appropriate price is $2.25.
Explanation:
There is 1 in 600 chance to win the grand price (1/600)
There are 2 in 600 chance to win the 2nd price (2/600 = 1/300)
There are 5 in 600 chance to win the 3rd price (5/600 = 1/120)
We can use these probability to calculate the expected gain from this game
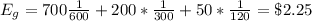
Since the cost to play is $3, the expected net gain from this game is
$2.25 - $3 = -$0.75
So this game is not fair as the player is losing money. The appropriate price should instead be $2.25