Question

Interactive Solution 9.37 presents a method for modeling this problem. Multiple-Concept Example 10 offers useful background for problems like this one. A cylinder is rotating about an axis that passes through the center of each circular end piece. The cylinder has a radius of 0.130 m, an angular speed of 78.0 rad/s, and a moment of inertia of 1.25 kg·m2. A brake shoe presses against the surface of the cylinder and applies a tangential frictional force to it. The frictional force reduces the angular speed of the cylinder by a factor of 6 during a time of 3.00 s. (a) Find the magnitude of the angular deceleration of the cylinder. (b) Find the magnitude of the force of friction applied by the brake shoe.

Answer 1

21.67 rad/s²

208.36538 N

Step-by-step explanation:

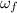`\omega_f` = Final angular velocity =
`(1)/(6)78=13\ rad/s`

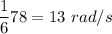
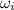`\omega_i` = Initial angular velocity = 78 rad/s

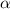`\alpha` = Angular acceleration

`\theta` = Angle of rotation

t = Time taken

r = Radius = 0.13

I = Moment of inertia = 1.25 kgm²

From equation of rotational motion

`\omega_f=\omega_i+\alpha t\\\Rightarrow \alpha=(\omega_f-\omega_i)/(t)\\\Rightarrow \alpha=(13-78)/(3)\\\Rightarrow \alpha=-21.67\ rad/s^2`

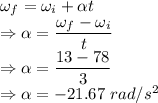
The magnitude of the angular deceleration of the cylinder is 21.67 rad/s²

Torque is given by

`\tau=I\alpha\\\Rightarrow \tau=1.25* -21.67\\\Rightarrow \tau=-27.0875`

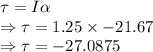
Frictional force is given by

`F=(\tau)/(r)\\\Rightarrow F=(-27.0875)/(0.13)\\\Rightarrow F=-208.36538\ N`

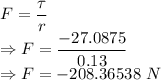
The magnitude of the force of friction applied by the brake shoe is 208.36538 N