Answer:
21.67 rad/s²
208.36538 N
Step-by-step explanation:
 = Final angular velocity =
= Final angular velocity =
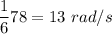
 = Initial angular velocity = 78 rad/s
= Initial angular velocity = 78 rad/s
 = Angular acceleration
= Angular acceleration
 = Angle of rotation
= Angle of rotation
t = Time taken
r = Radius = 0.13
I = Moment of inertia = 1.25 kgm²
From equation of rotational motion
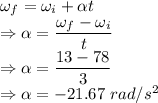
The magnitude of the angular deceleration of the cylinder is 21.67 rad/s²
Torque is given by

Frictional force is given by
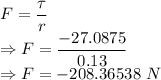
The magnitude of the force of friction applied by the brake shoe is 208.36538 N