Answer:
Option B.
Explanation:
The given equation is

Subtract both sides by 17.

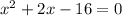 .... (1)
.... (1)
If a quadratic equation is
 , then by quadratic formula
, then by quadratic formula
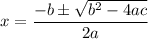
In equation (1), a=1, b=2 and c=-16. Using quadratic formula we get
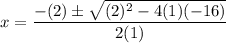
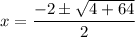

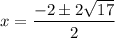
Taking out common factors.
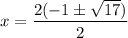
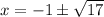
Therefore, the correct option is B.