Question

In a study of government financial aid for college​ students, it becomes necessary to estimate the percentage of​ full-time college students who earn a​ bachelor's degree in four years or less. Find the sample size needed to estimate that percentage. Use a0.04margin of error and use a confidence level of95​%.Assume that nothing is known about the percentage to be estimated.nequals=nothing​(Round up to the nearest​ integer.)

Answer 1

Answer: 601

Explanation:

When the prior estimate of the population proportion is unavailable , then the formula to find the sample size is given by :-

`n= 0.25((z^*)/(E))^2`

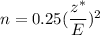
, where E = margin of error

and z* = Critical z-value associated with the confidence level.

As per given , we have

The prior percentage of​ full-time college students who earn a​ bachelor's degree in four years or less is not given.

E= 0.04

We know that the critical value for 95% confidence level = z*= 1.960

Then , the required sample size is given by :-

`n= 0.25((1.960)/(0.04))^2`

`n= 0.25(49)^2`

`n= 0.25(2401)=600.25\approx601`

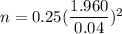
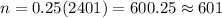
Hence, the required sample size is 601.