Answer:
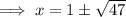
Explanation:
We want to solve for x in
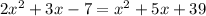
You need to group and combine like terms and write in standard form:
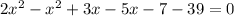
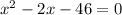
By comparing to
 , we a=1,b=-2 and c=-46
, we a=1,b=-2 and c=-46
The solution can be obtained using the quadratic formula.
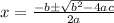
We substitute the coefficients to get:
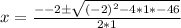
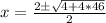
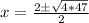

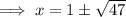
The last choice is correct