Question

Solve for x in the equation 2 x squared + 3 x minus 7 = x squared + 5 x + 39.

x = negative 6 plus-or-minus StartRoot 82 EndRoot
x = negative 6 plus-or-minus 2 StartRoot 17 EndRoot
x = 1 plus-or-minus StartRoot 33 EndRoot
x = 1 plus-or-minus StartRoot 47 EndRoot

Answer 1

D on edge 23

Explanation:

becasue i said so

Answer 2

`\implies x=1\pm √(47)`

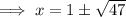
Explanation:

We want to solve for x in
`2x^2+3x-7=x^2+5x+39`

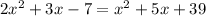
You need to group and combine like terms and write in standard form:

`2x^2-x^2+3x-5x-7-39=0`

`\imples x^2-2x-46=0`

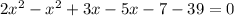
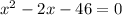
By comparing to
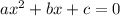`ax^2+bx+c=0`, we a=1,b=-2 and c=-46

The solution can be obtained using the quadratic formula.

`x=(-b\pm √(b^2-4ac) )/(2a)`

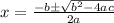
We substitute the coefficients to get:

`x=(--2\pm √((-2)^2-4*1*-46) )/(2*1)`

`x=(2\pm √(4+4*46) )/(2)`

`x=(2\pm √(4*47) )/(2)`

`x=(2\pm2√(47) )/(2)`

`\implies x=1\pm √(47)`

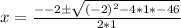
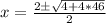
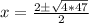
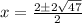
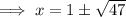
The last choice is correct