Question

An insulated piston-cylinder device contains 0.15 of saturated refrigerant-134a vapor at 0.8 MPa pressure. The refrigerant is now allowed to expand in a reversible manner until the pressure drops to 0.2 MPa. Determine the change in the exergy of the refrigerant during this process and the reversible work. Assume the surroundings to be at and 100 kPa.

Answer 1

Assumption:

1. The kinetic and potential energy changes are negligible

2. The cylinder is well insulated and thus heat transfer is negligible.

3. The thermal energy stored in the cylinder itself is negligible.

4. The process is stated to be reversible

Analysis:

a. This is reversible adiabatic(i.e isentropic) process and thus
`s_(1) =s_(2)`

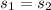
From the refrigerant table A11-A13

`P_(1) =0.8MPa`
`\left \{ {{ {{v_(1)=v_(g)  @0.8MPa =0.025645 m^(3/)/kg } } \atop { {{u_(1)=u_(g)  @0.8MPa =246.82 kJ/kg } -   also  {{s_(1)=s_(g)  @0.8MPa =0.91853 kJ/kgK } } \right.`

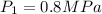
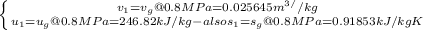
sat vapor

m=
`(V)/(v_(1) ) =(0.15)/(0.025645) =5.8491 kg\\and \\\\P_(2) =0.2MPa  \left \{ {{x_(2) =(s_(2) -s_(f) )/(s_(fg ))=(0.91853-0.15449)/(0.78339)   = 0.9753 \atop {u_(2) =u_(f) +x_(2) }(u_(fg)) =  38.26+0.9753(186.25)= 38.26+181.65 =219.9kJ/kg \right. \\s_(1) = s_(2)`

`T_(2) =T_(sat @ 0.2MPa) = -10.09^(o)  C`

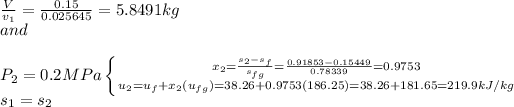
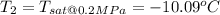
b.) We take the content of the cylinder as the sysytem.

This is a closed system since no mass leaves or enters.

Hence, the energy balance for adiabatic closed system can be expressed as:

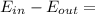`E_(in) - E_(out)  =`ΔE

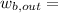`w_(b, out)  =`ΔU

`w_(b, out) =m([tex]u_(1) -u_{2`)

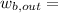`w_(b, out)  =` workdone during the isentropic process

=5.8491(246.82-219.9)

=5.8491(26.91)

=157.3993

=157.4kJ