Question

Apply the Pythagorean Theorem to find the distance between points A and C.

A)

29

units

Eliminate

B)

40

units

C)

58

units

D)

116

units

Answer 1

So the correct option is C ) 58 units.

Also If we require Distance then l(AC) = √58 = 7.615 units

Explanation:

Let the Points be

point A( x₁ , y₁) ≡ ( -2 , 1)

point C( x₂ , y₂) ≡ (5 , -2)

To Find:

d(AC) = ?

Solution:

By Applying the Pythagorean Theorem to find the distance between points A and C we get

`l(AC) = \sqrt{((x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2) )}`

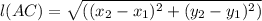
Substituting A( x₁ , y₁) ≡ ( -2 , 1) and C( x₂ , y₂) ≡ (5 , -2) we get

`l(AC) = \sqrt{((5-{(-2}))^(2)+(-2-1)^(2) )}\\\\l(AC) = \sqrt{(5+2)^(2)+(-3)^(2)}\\\\l(AC) = √((49+9))\\\\l(AC) = √(58)\\\\OR\\l(AC)^(2) = 58\ units`

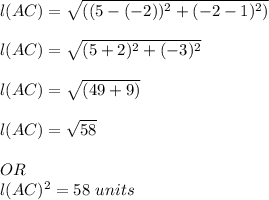
So the correct option is C ) 58 units.

If we require Distance then l(AC) = √58 = 7.615 units