Question

A manufacturer of lighting fixtures has daily production costs pf C(x)= 800- 10x+ 0.25x^2 , where C is the total cost in dollars and x is the number of units produced. Determine how many fixtures should be produced each day to yield minimum cost.

Answer 1

Answer: 20 fixtures

Explanation:

There are two methods to getting the number of fixtures to be produced.

Method 1

Given:

C(x) = 800 - 10x +
`0.25x^(2)`

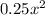
Re - arranging the function , we have

C(x) =
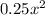`0.25x^(2)` - 10x + 800

This is a typical quadratic expression , since the coefficient of
`x^(2)` is positive , it means that the quadratic expression is a parabola that opens upward. We can therefore find the x - coordinate of the vertex of the parabola to find the number of fixtures that can be produced to yield minimum cost.

The formula for finding the x - coordinate of the vertex is give as
`(-b)/(2a)`

From the expression given , a = 0.25 , b = -10 , substituting into the formula , we have:

x =
`(-(-10))/(2(0.25))`

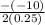
x = 10/0.5

x = 20

Therefore , 20 fixtures should be produced each day to yield minimum cost.

METHOD 2

This is the application of differential equation , the question means that we need to find the value of x for which the function is minimum. To do this , we will differentiate the function once with respect to x and equate to zero.

C(x) =
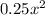`0.25x^(2)` - 10x + 800

differentiating once , we have

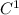`C^(1)`(x) = 0.5x - 10

setting it to zero , we have

0.5x - 10 = 0

0.5x = 10

x = 10/0.5

x = 20

This means that 20 fixtures should be produced each day to yield minimum cost.