Answer:
degree = 6
Explanation:
Given
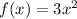 , and
, and
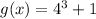 , we can find the composition of functions:
, we can find the composition of functions:
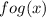 by applying the definition of composition and performing the needed algebra.
by applying the definition of composition and performing the needed algebra.
Recall that the composition of functions is defined as:
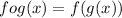 , where we use as input for the function f(x) the actual expression in terms of "x" of the function g(x):
, where we use as input for the function f(x) the actual expression in terms of "x" of the function g(x):
![f(g(x))=f(4x^3+1)\\f(g(x))=3(4x^3+1)^2\\f(g(x))=3\,(4x^3+1)\,(4x^3+1)\\f(g(x))=3\,[16x^6+4x^3+4x^3+1]\\f(g(x))=3\,[16x^6+8x^3+1]\\f(g(x))=48x^6+24x^3+3](https://img.qammunity.org/2020/formulas/mathematics/middle-school/mwsqgygev19i2sbtsj2vk79neo3ii663iz.png)
Therefore, the degree of this expression is "6" (the highest power at which the variable "x" appears)