Question

John works two jobs. As a security guard he earns $8.50 per hour. As a landscaper he earns $14 per hour. One week John worked a total of 60 hours and earned $691.50. How many hours did he work at each job?

Answer 1

28, 32

Explanation:

Answer 2

John work as a security guard job 27 hours and as a landscaper 33 hours.

Explanation:

Given:

John works two jobs.

As a security guard he earns $8.50 per hour and as a landscaper he earns $14 per hour.

One week John worked a total of 60 hours and earned $691.50.

Now, to find hours he work at each job.

Let the job of security guard be
`x` hours.

And the job of landscaper be
`y` hours.

So, the total hours John worked in a week:

`x+y=60.`

⇒
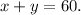
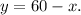`y=60-x.`............( 1 )

Now, the money earned by John in a week:

`8.50x+14y=691.50`

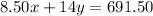
Putting the equation ( 1 ) in the place of
`y`:

⇒
`8.50x+14(60-x)=691.50`

⇒
`8.50x+840-14x=691.50`

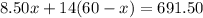
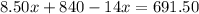
Moving variables on one side and the other we get:

⇒
`840-691.50=14 x-8.50x`

⇒
`148.50=5.50x`

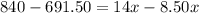
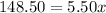
Dividing both sides by 5.50 we get:

⇒
`27=x`

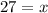
As a security guard job he worked 27 hours.

Putting the value of in
`x` equation ( 1 ) we get:

`y=60-27`

⇒
`y=33.`

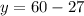
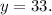
As a landscaper he worked 33 hours.

Therefore, John work as a security guard job 27 hours and as a landscaper 33 hours.