Question

A recent study by Ohio State University reported at Science Daily suggests that students with cell phones may take more risks than students that do not have cell phones. In a sample of 305 Ohio State University female students, 128 (42%) responded that if they had a cell phone, they would be willing to walk somewhere after dark that they would normally not go.

Use the above survey results to test the hypotheses
H0: p = 0.50
HA: p < 0.50
where p is the proportion of female students who, if they had a cell phone, would be willing to walk somewhere after dark that they would normally not go.

Question 1. What is the value of the test statistic z for this hypothesis test? (Use 2 decimal places in your answer).

Answer 1

The value of the test statistic z for this hypothesis test is -2.79

Explanation:

Consider the provided information.

To calculate the test statistic use the formula:

`z=\frac{\hat p-p_0}{\sqrt{(p_0(1-p_0))/(n)}}`

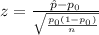
Where, z is Test statistics, n is Sample size, p₀ = Null hypothesized value and
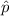`\hat p` = Observed proportion.

p₀ = 0.50

Thus 1-p₀= 0.50

42% responded that if they had a cell phone, thus
`\hat p=0.42`

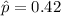
The sample size is 305.

Substitute the respective values in the above formula.

`z=\frac{0.42-0.50}{\sqrt{(0.50(0.50))/(305)}}`

`z=(-0.08)/(√(0.00082))`

`z=-2.79`

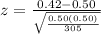
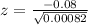
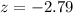
Hence, the value of the test statistic z for this hypothesis test is -2.79