Answer:
The value of the test statistic z for this hypothesis test is -2.79
Explanation:
Consider the provided information.
To calculate the test statistic use the formula:
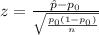
Where, z is Test statistics, n is Sample size, p₀ = Null hypothesized value and
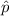 = Observed proportion.
= Observed proportion.
p₀ = 0.50
Thus 1-p₀= 0.50
42% responded that if they had a cell phone, thus
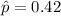
The sample size is 305.
Substitute the respective values in the above formula.
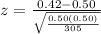
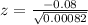
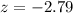
Hence, the value of the test statistic z for this hypothesis test is -2.79