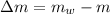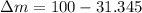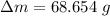Question

600-g of ice at −15℃ is in a calorimeter when 100 g of water at 20℃ is added to it. Water cools down and part of it freezes as a result. Find the mass of the remaining liquid water. Neglect the heat capacity of the calorimeter. [
`c_i` = 0.5 cal/g/℃ = 2090 J/kg/℃,
`c_w` = 1 cal/g/℃ = 4186J/kg/℃,
`L_f` = 79.7 cal/g = 3.33 × 10⁵ J/kg]

Answer 1

`\Delta m =68.654\ g`

Step-by-step explanation:

Given:

• mass of ice,
  `m_i=600\ g`

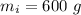
• initial temperature of ice,
  `T_(ii)=-15\ ^(\circ)C`

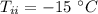
• mass of water added,
  `m_w=100\ g`

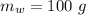
• initial temperature of water,
  `T_(iw)=20\ ^(\circ)C`

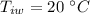
• specific heat capacity of ice,
  `c_i=2.090\ J.g^(-1).^(\circ)C^(-1)`

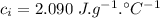
• specific heat capacity of water,
  `c_w=4.186\ J.g^(-1).^(\circ)C^(-1)`

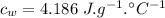
• latent heat of fusion,
  `L_f=333\ J.g^(-1)`

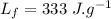
According to question a part of water freezes while the other remains liquid:

So,

final temperature of the mixture,
`T_f=0 ^(\circ)C`

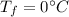
Now using the equation of heat:

Heat required by the total ice of given temperature to melt completely:

`Q_i=m_i.c_i.\Delta T`

`Q_i=600* 2.090* (0-(-15))`

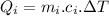
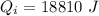`Q_i=18810\ J` .....................................(1)

Heat released by the total mass of given water to come to freezing point:

`Q_w=m_w.c_w.\Delta T`

`Q_w=100* 4.186* (20)`

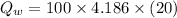
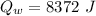`Q_w=8372\ J` ...............................................(2)

Now from the eq. (1) & (2) the difference in heat is equivalent to the mass of water frozen.

`\Delta Q=Q_i-Q_w`

`\Delta Q=18810-8372`

`\Delta Q=10438\ J`

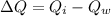
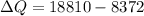
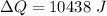
Now the mass of water frozen:

`\Delta Q = m.L_f`

`m=(\Delta Q)/(L_f)`

`m=(10438)/(333)`

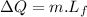
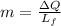
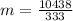
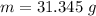`m=31.345\ g` of more ice is formed from the water.

Mass of remaining liquid:

`\Delta m =m_w-m`

`\Delta m =100-31.345`

`\Delta m =68.654\ g`