Answer:
30643 J
Step-by-step explanation:
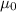 = Vacuum permeability =
= Vacuum permeability =
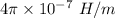
t = Time taken = 1 ns
c = Speed of light =
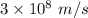
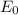 = Maximum electric field strength =
= Maximum electric field strength =
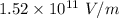
A = Area =
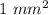
Magnitude of magnetic field is given by
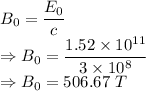
Intensity is given by
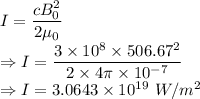
Power, intensity and time have the relation

The energy it delivers is 30643 J