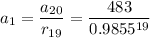Answer:
The first contribution was 637.77
Explanation:
Geometric Sequences
It a type sequence in which each term is computed as the previous term by a constant number. The general expression for a geometric sequence is
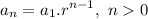
If we know two terms of the sequence, say n=k and n=p, then
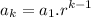
and
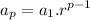
We can determine the values of
 and r, by manipulating both equations
and r, by manipulating both equations
We know that
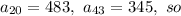

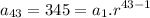
Dividing both expressions, we have
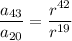
Solving for r
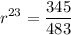
![\displaystyle r=\sqrt[23]{(345)/(483)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/z4c9w1dcohdwhimiv391qw8g3p82swbv7c.png)
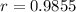
Now we use

to compute