Answer:
The simplified form is
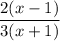 .
.
 is the excluded value for the given expression.
is the excluded value for the given expression.
Explanation:
Given:
The expression given is:
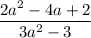
Let us simplify the numerator and denominator separately.
The numerator is given as
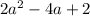
2 is a common factor in all the three terms. So, we factor it out. This gives,

Now,
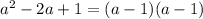
Therefore, the numerator becomes
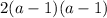
The denominator is given as:
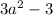
Factoring out 3, we get
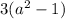
Now,
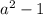 is of the form
is of the form
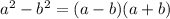
So,
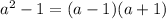
Therefore, the denominator becomes
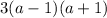
Now, the given expression is simplified to:

There is
 in the numerator and denominator. We can cancel them only if
in the numerator and denominator. We can cancel them only if
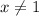 as for
as for
 , the given expression is undefined.
, the given expression is undefined.
Now, cancelling the like terms considering
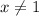 , we get:
, we get:
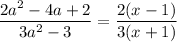
Therefore, the simplified form is
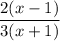
The simplification is true only if
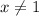 . So,
. So,
 is the excluded value for the given expression.
is the excluded value for the given expression.