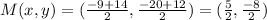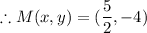Answer:
The midpoint of segment AB is
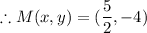
Explanation:
Given:
Let the end points be
point A( x₁ , y₁) ≡ ( -9 , -20)
point B( x₂ , y₂) ≡ (14 , 12)
M( x , y ) be the Mid point of AB
To Find:
M( x , y ) = ?
Solution:
If M is the midpoint of segment AB then by midpoint formula the M coordinates are given by,
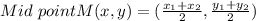
On substituting the values in above formula we get