Answer:
B.
![(b)/(2a^(2)c^3)\sqrt[3]{15b}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/z22rzbja3usxmwlut5sczkihuivlkrqasm.png)
Explanation:
Given:
The expression to simplify is given as:
![\sqrt[3]{(75a^7b^4)/(40a^(13)c^9)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/kp7wi2dxntx7izzloepl1vlssqdnf8pafg.png)
Use the exponent property
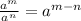
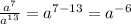
Use the exponent property
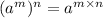
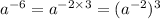
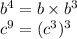
Reducing
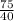 to simplest form, we get:
to simplest form, we get:
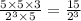
Therefore, expression becomes:
![\sqrt[3]{(15(a^(-2))^3* b* b^3)/(2^3(c^3)^3)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/fvdjsirn1qojl8jn8feh27oxgwhjnol04l.png)
Use the cubic root property:
![\sqrt[3]{x^3} =x](https://img.qammunity.org/2020/formulas/mathematics/middle-school/5ivby3cc0qomiy736uf2m6kd9cn3bpgx32.png) . Thus, the expression becomes:
. Thus, the expression becomes:
![(a^(-2)b)/(2c^3)\sqrt[3]{15b}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/2rwlyl26cm4hoggecqtf1ldp59ddgqxy1y.png)
Using the exponent property
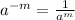
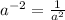
So, the final expression is:
![(b)/(2a^(2)c^3)\sqrt[3]{15b}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/z22rzbja3usxmwlut5sczkihuivlkrqasm.png)
Therefore, the correct option is option B.