Question

Anystate Auto Insurance Company took a random sample of 360 insurance claims paid out during a 1-year period. The average claim paid was $1510. Assume σ = $236. Find a 0.90 confidence interval for the mean claim payment. (Round your answers to two decimal places.) lower limit $ upper limit $ Find a 0.99 confidence interval for the mean claim payment. (Round your answers to two decimal places.) lower limit $ upper limit $

Answer 1

Answer with explanation:

The formula to find the confidence interval is given by :-

`\overline{x}\pm z^*SE.`

, where
`\overline{x}` = Sample mean

z* = Critical value.

SE = Standard error ,
`SE=(\sigma)/(√(n))`,
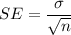`\sigma` = Population standard deviation.

n= Sample size.

As per given , we have

`\overline{x}=\$1510`

`\sigma=\$236`

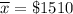
n= 360

`SE=(236)/(√(360))=(236)/(18.973665961)\\\\=12.43829213\approx12.49`

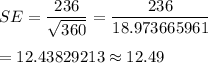
We know that the critical value for 0.90 confidence interval : z* = 1.645

Then, a 0.90 confidence interval for the mean claim payment.will be :

`1510\pm (1.645)(12.49)\\\\ =1510\pm20.54605\\\\=(1510-20.54605,\ 1510+20.54605)\\\\=(1489.45395,\ 1530.54605)\approx(1489.45,\ 1530.55)`

∴ a 0.90 confidence interval for the mean claim payment. = ($1489.45,$1530.55)

We know that the critical value for 0.99 confidence interval : z* = 2.576

0.99 confidence interval for the mean claim payment will be :

`1510\pm (2.576)(12.49)\\\\ =1510\pm32.17424\\\\=(1510-32.17424,\ 1510+32.17424)\\\\=(1477.82576,\ 1542.17424)\approx(1477.83,\ 1542.17)`

∴ a 0.99 confidence interval for the mean claim payment. = ($1477.83, $1542.17)