Answer with explanation:
The formula to find the confidence interval is given by :-
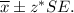
, where
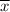 = Sample mean
= Sample mean
z* = Critical value.
SE = Standard error ,
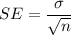 ,
,
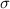 = Population standard deviation.
= Population standard deviation.
n= Sample size.
As per given , we have
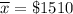
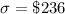
n= 360
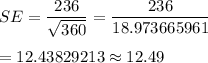
We know that the critical value for 0.90 confidence interval : z* = 1.645
Then, a 0.90 confidence interval for the mean claim payment.will be :

∴ a 0.90 confidence interval for the mean claim payment. = ($1489.45,$1530.55)
We know that the critical value for 0.99 confidence interval : z* = 2.576
0.99 confidence interval for the mean claim payment will be :

∴ a 0.99 confidence interval for the mean claim payment. = ($1477.83, $1542.17)